Symetralna odcinka – teoria

Wyobraź sobie, że na pustej kartce pojawią się dwa punkty $A$ i $B$. Połącz je ze sobą – masz już odcinek.
Znajdź punkt $C$, który dzieli odcinek $AB$ na pół
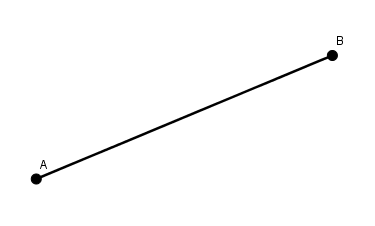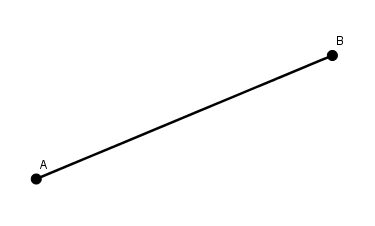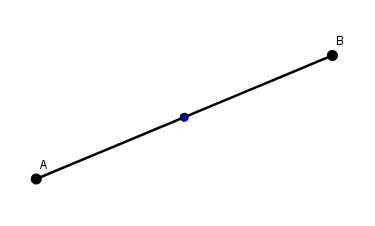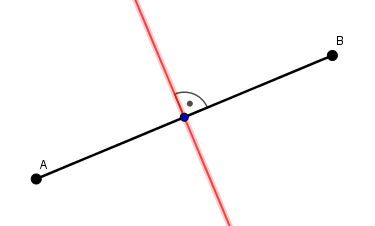
(czyli $AC=BC$). Przez punkt $C$ poprowadź prostą prostopadłą do odcinka $AB$.
Symetralna odcinka jest tą prostą 🙂

 

Symetralna odcinka – prosta prostopadła do danego odcinka, która przechodzi
przez jego środek.

Wyznaczanie symetralnej odcinka

Przykład: Znajdź symetralną odcinka $AB$, gdzie $A=(-2,4)$ i $B=(2,2)$.

Na początek wyznaczmy równanie prostej przechodzącej przez dwa punkty $A$ i $B$.


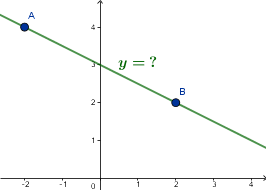
Podstawmy do wzoru: $(y-y_a)(x_b-x_a)-(y_b-y_a)(x-x_a)=0$
gdzie $x_a=-2$, $y_a=4$, $x_b=2$, $y_b=2$.

Mamy:
$(y-y_a)(x_b-x_a)-(y_b-y_a)(x-x_a)$$=(y-4)(2-(-2))-(2-4)(x-(-2))$$=(y-4)\cdot 4+2\cdot (x+2)$$=4(y-4)+2(x+2)$$=4y-16+2x+4$$=2x+4y-12$$=0$
$$4y=-2x+12$$
$$y=-\frac12x+3$$

Symetralna odcinka jest prostą prostopadłą do prostej $y=-\frac12x+3$ zatem współczynik kierunkowy symetralnej wynosi $2$. ($2$ jest odwrotna i przeciwna do $-\frac12$) Skąd to wiemy?

Symetralna odcinka przechodzi przez jego środek. Korzystamy ze wzoru:

$$S=(\frac{x_a+x_b}2,\frac{y_a+y_b}2)$$

$$S=(\frac{-2+2}2,\frac{4+2}2)$$

$$S=(0,3)$$

Wiemy więc, że symetralna przechodzi przez punkt $S=(0,3)$ oraz z prostopadłości wyraża się wzorem:$$y=2x+b$$

Podstawmy współrzędne punktu $S$ do wzoru:

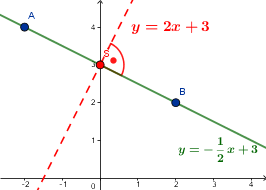$$y=2\cdot x+b$$

$$3=2\cdot 0+b$$

$$3=0+b$$

$$b=0$$

$$y=2x+3$$

Odpowiedź: Symetralna odcinka $AB$ zdefiniowana jest wzorem $y=2x+3$.

Uwaga: Symetralna odcinka krok po kroku.

Jeżeli szukasz symetralnej odcinka $AB$, a w poleceniu widzisz współrzędne punktów $A$ i $B$ postępuj według następującego schematu:

$1°$ Znajdź prostą przechodzącą przez punkty $A$ i $B$.

$2°$ Znajdź współczynnik kierunkowy prostej prostopadłej do niej.

$3°$ Znajdź środek odcinka $AB$.

$4°$ Znając współczynnik z $2°$ oraz punkt z $3°$ otrzymasz równanie symetralnej.

Symetralna odcinka – zastosowanie w zadaniach

Przykład: Podstawą trójkąta równoramiennego $ABC$ jest bok $AB$, gdzie $A=(1,2)$ i $B=(4,3)$. Ramię tego trójkąta zawiera się w prostej o równaniu $y=x-1$. Oblicz współrzędne wierzchołka $C$.

Zanim przejdziemy do rozwiązania przykładu wykonajmy rysunek zawierający wszystkie dane z polecenia. Dzięki temu rozwiązanie będzie bardziej intuicyjne 🙂


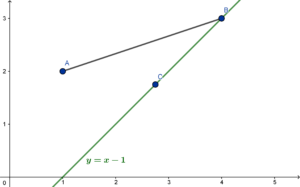
Widzimy teraz, że podstawą do rozwiązania zadania jest znalezienie stycznej odcinka $AB$. Skorzystajmy z powyższej uwagi.

$1°$ Wyznaczmy prostą przechodzącą przez punkty $A=(1,2)$ i $B=(4,3)$.

Mamy:
$(y-y_a)(x_b-x_a)-(y_b-y_a)(x-x_a)$$=(y-1)(4-1)-(3-2)(x-1)$$=-x+3y-5=0$

$3y=x+5$

$y=\frac13x+ \frac53$

$2°$ Wyznaczmy współczynnik kierunkowy prostej prostopadłej do prostej $y=\frac13x+ \frac53$.

Współczynnik kierunkowy prostej $y=\frac13x+ \frac53$ to $\frac13$.

Liczbą odwrotną do $\frac13$ jest $3$.

Liczbą przeciwną do $3$ jest $-3$.

Ostatecznie szukana styczna jest postaci $y=-3x+b$.

$3°$ Szukamy środka odcinka $AB$.

Skoro $A=(1,2)$ i $B=(4,3)$, to środek odcinka $AB$ to $S=\frac52, \frac52$.

$4°$ Skoro prosta $=-3x+b$ przechodzi punkt $S=(\frac52, \frac52)$ otrzymujemy, że:

$$\frac52=-3\cdot \frac52 + b$$

$$\frac52=-\frac{15}2 + 2|\cdot 2$$

$$\frac{20}2=b$$

$$b=10$$

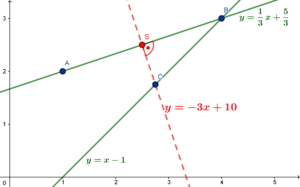
Ostatecznie symetralna odcinka $AB$ jest postaci $y=-3x+10$

Znamy równanie stycznej do odcinka $AB$.
Jak dzięki temu wyznaczyć współrzędne punktu $C$?
Z rysunku wnioskujemy, że punkt $C$ jest punktem przecięcia znalezionej stycznej oraz prostej $y=x-1$.
Rozwiązujemy następujące równanie:
$$\left\{\begin{array}{l}y=-3x+10\\y=x-1\end{array}\right.$$Z drugiego równania wyznaczamy $x$$$\left\{\begin{array}{l}y=-3x+10\\x=y+1\end{array}\right.$$Podstawiamy $x$ do pierwszego rówaniania$$y=-3(y+1)+10$$$$y=-3y-3+10$$$$4y=7$$$$y=\frac74$$Podstawmy $y$ do równania $x=y+1$$$x=\frac74+1=\frac{11}4$$.
Ostatecznie punkt C ma następujące współrzędne: $x=\frac{11}4$, $y=\frac74$.
Odpowiedź: Współrzędne wierzchołka $C$ wynoszą $(\frac{11}4,\frac74)$.
12+
Anita Księżak