Walec

Walec jest bryłą obrotową powstałą z obrotu o $360^\circ $ prostokąta o bokach $r, h$ dookoła prostej zawierającej bok $h.$ Bok prostokąta $h$ nazywamy wysokością walca, a bok $r$ jest promieniem podstawy walca.
Zwróćmy uwagę na to, jak wygląda siatka walca i jakie są jej wymiary.

Przekrój osiowy walca

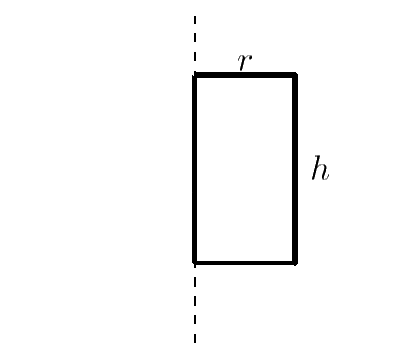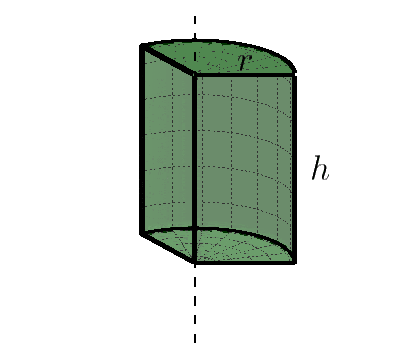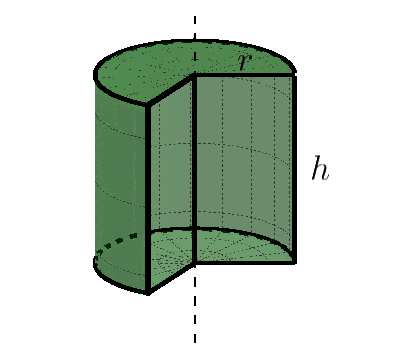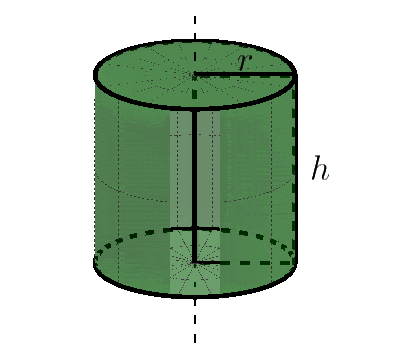
Przekrojem osiowym walca nazywamy prostokąt zawarty w tym walcu o bokach długości $2r$ oraz $h.$

Jeśli wyobrazimy sobie, że nasz walec jest tortem, to przekrój osiowy walca będzie prostokątem, który widzimy, gdy ktoś przekroi tort dokładnie na pół, tnąc równolegle do osi obrotu.

Objętość walca

Objętość walca liczymy podobne jak przy graniastosłupach korzystając ze wzoru:
$$Objętość\: walca=Pole\: podstawy \cdot wysokość$$
Różnica polega na tym, że podstawą walca jest koło, zatem:

Objętość walca wyraża się wzorem:
$$V=\underbrace{\pi r^2}_{Pole\: podstawy}\cdot h$$

Pole powierzchni bocznej walca\Pole powierzchni całkowitej walca

Jak można odczytać z zamieszczonego wyżej rysunku siatki, po „rozwinięciu” walca powierzchnią boczną walca jest prostokąt o wymiarach $h$ na $2\pi r.$

Pole powierzchni bocznej walca wyraża się wzorem:
$$P_{B}=h\cdot 2\pi r$$

Pole powierzchni całkowitej walca określa się jako:

$Pole\: powierzchni\: całkowitej = $$Pole\: powierzchni\: bocznej + $$2\cdot Pole\: podstawy$

Czyli po prostu:

Pole powierzchni całkowitej walca określa się wzorem:
$$P_{C}=2\cdot \pi r^2+h\cdot 2\pi r$$
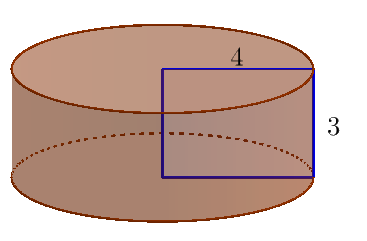
Przykład 1: Oblicz objętość i pole powierzchni całkowitej walca powstałego z obrotu prostokąta o wymiarach 3 na 4 wokół prostej zawierającej bok o długości 3.
Narysujmy obrazek poglądowy:

Ze wzoru na objętość walca mamy:
$V=\pi 4^2\cdot 3=48\pi $
Ze wzoru na pole powierzchni całkowitej walca mamy:
$P_{C}=2\pi \cdot 4^2+3\cdot 2\pi \cdot 4= 32\pi +24\pi =56\pi$
Odpowiedź: Objętość tego walca to $48\pi ,$ a jego pole powierzchni całkowitej, to $56\pi .$
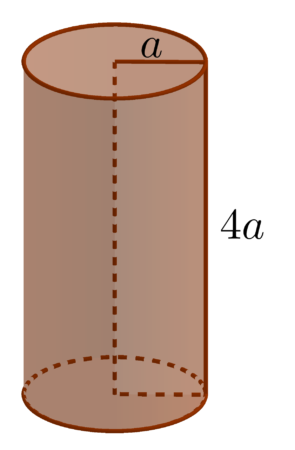
Przykład 2: Objętość walca, w którym wysokość jest czterokrotnie dłuższa od promienia jest równa 32. Oblicz promień podstawy tego walca.
Narysujmy obrazek poglądowy:

Z treści zadania wiemy, że $V=32$
Ze wzoru na objętość walca mamy:
$V=\pi a^2\cdot 4a=4a^3\pi$
Zatem:
$32=4a^3 \quad \mid :4$
$8=a^3 \pi \quad \mid :\pi $
$a^3=\frac{8}{\pi}$
$a=\sqrt[3]{\frac{8}{\pi}}$
Odpowiedź: Promień podstawy tego walca ma długość $\sqrt[3]{\frac{8}{\pi}}$
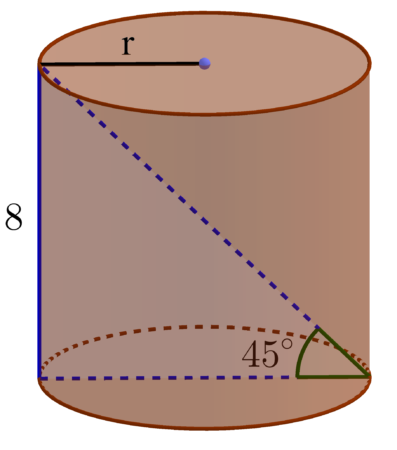
Przykład 3: Przekątna przekroju osiowego walca jest nachylona do jego płaszczyzny podstawy pod kątem $45^{\circ }.$ Wysokość tego walca ma długość 8. Oblicz objętość podanego walca.
Narysujmy obrazek poglądowy:

Ponieważ przekątna przekroju osiowego walca jest nachylona do płaszczyzny jego podstawy pod kątem $45^{\circ },$ sam przekrój osiowy walca jest kwadratem, stąd mamy:
$2r=8 \mid :2$
$r=4$

Alternatywnie możemy dojść do tego samego wyniku w poniższy sposób:
$sin45^{\circ }=\frac{8}{2r}$
$1=\frac{8}{2r} \quad \mid \cdot r$
$r=4$

Stąd i ze wzoru na objętość walca mamy:
$V=\pi 4^2\cdot 8=128\pi $
Odpowiedź: Objętość tego walca jest równa $128\pi .$

Przykład 4:Oblicz objętość walca, jeśli wiadomo, że jego pole powierzchni bocznej jest równe $16\pi $ a jego wysokość ma długość 4.
Ze wzoru na pole powierzchni bocznej walca mamy:
$4\cdot 2\pi r= 16\pi \mid :\pi $
$8r=16 \quad \mid :8$
$r=2$
Zatem po podstawieniu do wzoru mamy:
$V=\pi \cdot 2^2\cdot 4=16\pi $
Odpowiedź: Objętość tego walca, to $16\pi .$
1+
Tobiasz Tomaszewski