Graniastosłup prawidłowy czworokątny
Graniastosłupem prawidłowym czworokątnym nazywamy graniastosłup, którego podstawą jest kwadrat, oraz wszystkie jego ściany boczne są prostokątami prostopadłymi do krawędzi podstawy.
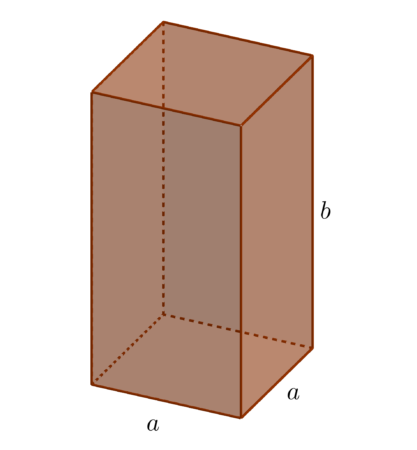

Zauważmy, że graniastosłup prawidłowy czworokątny jest szczególnym przypadkiem prostopadłościanu.
Graniastosłup prawidłowy czworokątny ma zawsze:
- 6 ścian
- 12 krawędzi
- 8 wierzchołków
Objętość graniastosłupa prawidłowego czworokątnego
Objętość graniastosłupa liczymy wzorem:
$Objętość=Pole\: podstawy \cdot wysokość$
W przypadku graniastosłupa prawidłowego czworokątnego mamy:
$Pole\: podstawy=a^2$
Zatem:
Objętość graniastosłupa prawidłowego czworokątnego określa się wzorem:
$$V=a^2\cdot b$$
gdzie $a,b$ to długości krawędzi graniastosłupa prawidłowego czworokątnego($a$ odpowiada długości krawędzi podstawy).
$$V=a^2\cdot b$$
gdzie $a,b$ to długości krawędzi graniastosłupa prawidłowego czworokątnego($a$ odpowiada długości krawędzi podstawy).
Pole powierzchni całkowitej granistosłupa prawidłowego czworokątnego
$Pole\: powierzchni\: całkowitej=Pole\: powierzchni\: bocznej+2\cdot Pole\: podstawy$
$Pole\: powierzchni\: bocznej=ab+ab+ab+ab=4 \cdot ab$
$Pole\: podstawy=a^2$
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego określa wzór:
$$P_{C}=2\cdot a^2+4\cdot ab$$
gdzie $a,b$ to długości krawędzi graniastosłupa prawidłowego czworokątnego($a$ odpowiada długości krawędzi podstawy).
$$P_{C}=2\cdot a^2+4\cdot ab$$
gdzie $a,b$ to długości krawędzi graniastosłupa prawidłowego czworokątnego($a$ odpowiada długości krawędzi podstawy).
Przykład 1: Graniastosłup prawidłowy czworokątny ma krawędzie podstawy długości 4, oraz wysokość długości 8. Oblicz pole powierzchni całkowitej oraz objętość tego graniastosłupa.
Narysujmy obrazek poglądowy:
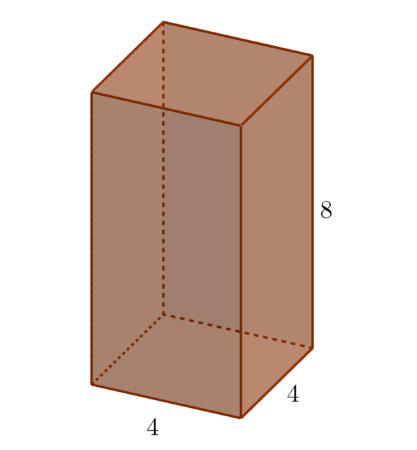
Podstawiając pod wzory na pole powierzchni całkowitej i objętość graniastosłupa prawidłowego czworokątnego otrzymujemy:
$P_{C}=2\cdot 4^2+4\cdot 4\cdot 8=32+128=160$
$V=4^2\cdot 8=128$
Odpowiedź:Pole powierzchni całkowitej tego graniastosłupa to 160, a jest objętość, to 128.

Podstawiając pod wzory na pole powierzchni całkowitej i objętość graniastosłupa prawidłowego czworokątnego otrzymujemy:
$P_{C}=2\cdot 4^2+4\cdot 4\cdot 8=32+128=160$
$V=4^2\cdot 8=128$
Odpowiedź:Pole powierzchni całkowitej tego graniastosłupa to 160, a jest objętość, to 128.
Przykład 2: Graniastosłup prawidłowy czworokątny ma pole powierzchni całkowitej równe 176, oraz wysokość długości 9. Oblicz długość krawędzi podstawy tego graniastosłupa.
Narysujmy obrazek poglądowy:
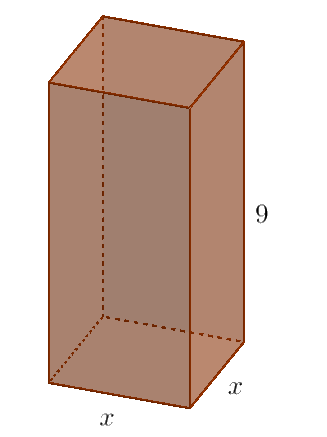
Z treści zadania wiemy, że $P_{C}=176,$ zatem
$176=2x^2+4\cdot 9x$
$2x^2+36x-176=0$
Rozwiązanie tego równania jest równoważne znalezieniu miejsc zerowych funkcji kwadratowej $f(x)=2x^2+36x-176$

Z treści zadania wiemy, że $P_{C}=176,$ zatem
$176=2x^2+4\cdot 9x$
$2x^2+36x-176=0$
Rozwiązanie tego równania jest równoważne znalezieniu miejsc zerowych funkcji kwadratowej $f(x)=2x^2+36x-176$
$\Delta =b^2-4ac=36^2-4\cdot 2 \cdot (-176)=1296+1408=2704$
$\sqrt{\Delta}=52$
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-36-52}{2\cdot 2}=-22$
$x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-36+52}{2\cdot 2}=4$
Ponieważ długość musi być nieujemna interesujący nas wynik, to $x_2,$ zatem $x=x_2=4$
Odpowiedź: Długość krawędzi podstawy podanego graniastosłupa to 4.
Przykład 3: Przekątna graniastosłupa prawidłowego czworokątnego o wysokości długości 10, jest nachylona do płaszczyzny jego podstawy pod kątem $45^{\circ}.$ Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
Narysujmy obrazek poglądowy:
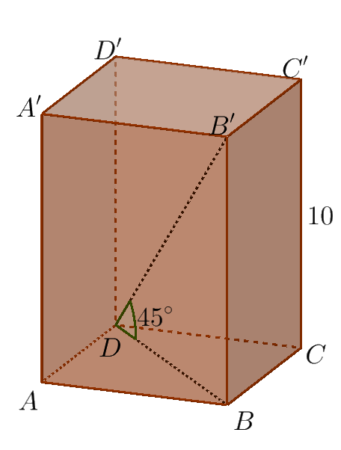
Narysujmy dodatkowo kwadrat $ABCD,$ oraz trójkąt $DBB^{\prime}$

Na początek zauważmy, że trójkąt $DBB^{\prime}$ jest połową kwadratu o boku długości 10. Mamy zatem $\mid DB\mid = \mid BB^{\prime}\mid =10.$
Odcinek $DB$ jest przekątną kwadratu $ABCD,$ stąd i z wiedzy, że przekątna kwadratu o boku długości $a$ ma długość $a\sqrt2$ możemy łatwo wyznaczyć długość boku tego kwadratu,
$\mid AB\mid \cdot \sqrt2 = \mid DB\mid$
$\mid AB\mid \cdot \sqrt2 =10 \quad \mid :\sqrt2$
$\mid AB\mid =\frac{10}{\sqrt2}=\frac{10\sqrt2}{2}=5\sqrt2$
Mając długość odcinka $AB$ możemy obliczyć pole powierzchni całkowitej i objętość podanego graniastosłupa.

Narysujmy dodatkowo kwadrat $ABCD,$ oraz trójkąt $DBB^{\prime}$
Na początek zauważmy, że trójkąt $DBB^{\prime}$ jest połową kwadratu o boku długości 10. Mamy zatem $\mid DB\mid = \mid BB^{\prime}\mid =10.$
Odcinek $DB$ jest przekątną kwadratu $ABCD,$ stąd i z wiedzy, że przekątna kwadratu o boku długości $a$ ma długość $a\sqrt2$ możemy łatwo wyznaczyć długość boku tego kwadratu,
$\mid AB\mid \cdot \sqrt2 = \mid DB\mid$
$\mid AB\mid \cdot \sqrt2 =10 \quad \mid :\sqrt2$
$\mid AB\mid =\frac{10}{\sqrt2}=\frac{10\sqrt2}{2}=5\sqrt2$
Mając długość odcinka $AB$ możemy obliczyć pole powierzchni całkowitej i objętość podanego graniastosłupa.
$P_{C}=2(5\sqrt2)^2+4\cdot 10 \cdot 5\sqrt2=100+200\sqrt2$
$V=(5\sqrt2)^2\cdot 10=500$
Odpowiedź: Pole powierzchni całkowitej tego graniastosłupa to $100+200\sqrt2,$ a jego objętość to $500.$

Matura z matematyki?
Oferujemy SuperKorepetycje - korki online połączone z przejrzyście zrozumiałymi filmikami do nauki własnej
Zobacz więcej4+
